池田： 浜松学芸中学校の3年生の時から数学の探究活動に所属しています。中学2年の時に、当時の高校3年生が数学オリンピックで受賞して「この学校にもこんなにすごい人がいるんだ」と思ったのがきっかけです。今も数学探究の活動の一つとして、数学オリンピックの予選に向けた準備を行っています。

宇都： 数学オリンピックや数学甲子園をめざしているので、数学探究では高3で習うようなレベルの高い内容に取り組んでいます。中3から入ってくる生徒もたまにいて、その一人が池田君です。彼は中3の時、中学生向けの「ジュニア数学オリンピック」で東海地区の優秀賞を受賞しています。

池田： 探究活動とは別に、個人的に取り組んでいるのが数学の研究です。「数論」と言って、自然数や約数、素数など、「数」についていろいろなことを考えています。そこで自主的に研究したことを、探究部活動オープンスクールでプレゼンテーションしました。

宇都： 内容を説明するのがなかなか難しいのですが、彼がある関数について、興味深い事実を見つけたんです。（ここで池田さんが黒板に数式を書く）

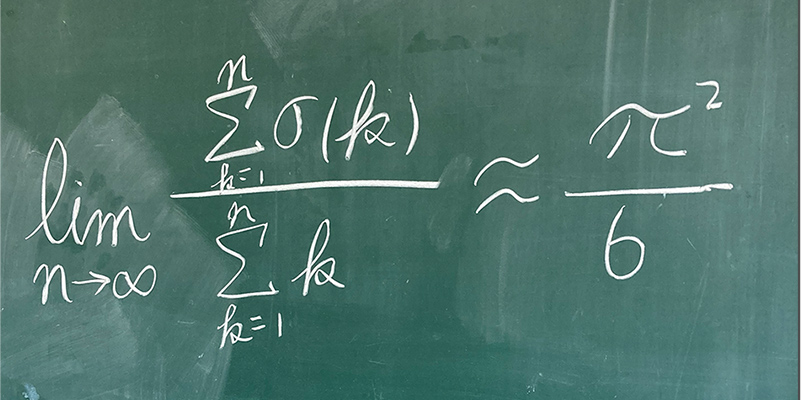
池田： この数式で、左側の分数の分子が「約数関数」というもので、ある自然数の約数を全部足したものになります。たとえば「6」だとしたら、6の約数は1と2と3と6なので、全部足すと12になります。「σ（シグマ）6」というのは12を表すんです。で、その自然数が1から順に増えていくに従い、約数関数の値を「σ1＋σ2＋σ3＋……」と全部足していきます。一方で、分母は1からｎまでの自然数を足したものを表しています。その分母で分子を割ると、nの数が増えるにつれてどんどん6分のΠ（パイ）二乗に近づいていきます。）

宇都： パイというのは、半径1の円の円周の半分の長さのことです。パイは無理数と言って、小数点以下の数字が規則性なく延々と続いていきます。で、池田君の数式では、「整数を足し続けていったもの」を「整数を足し続けていったもの」で割っているのに、その数が大きくなっていくとなぜか円周の長さに近づいていく。「何で突然円周の長さが出てくるの？」という、とても興味深い事実なんです。

池田： 家のパソコンで計算しました。たとえば「ｎ＝100万」という時に100万という自然数の約数を自分で全部足していくことはほぼ不可能ですが、プログラミングを使えば計算できます。それで最終的に出てきたのが、1.64493……という数字です。それが何にあたるかを調べると、6分のΠ（パイ）二乗だったのです。分かった時は「えっ！」と驚きました。それで宇都先生に見せに行きました。

宇都： この研究内容を見せられた時はびっくりしましたね。大学の数学科で数論を専門にしている人が取り組むような内容ですから。もちろん、私自身も専門分野ではありません。池田君は「今後はこの証明を試みたい」と言っていたのですが、しばらくして「先生、ダメでした。100年前に見つけられていました」と言ってきました。

池田： そうなんです。ネットでいろいろ調べたところ、100年ほど前の数学者がすでに証明していたことが分かったんです。

池田： 「自分しか見たことのない景色」が見えるところに、研究の面白さを感じます。他の人が絶対に考えていないようなことを考えて、自分にしかできない結果を出す。それが楽しくて、研究に取り組んでいます。もちろん、数学オリンピックで出題されるような数学も、授業で学ぶ数学も好きです。高校数学の範囲はほぼ学習が終わっていて、今後は大学でやるような数学を勉強してみようかと思っています。

宇都： 彼のすごいところは、自分で“勝手に”学んでいくところです。英検も準1級に合格しましたし、プログラミングも自分で勉強しています。主体性というか、どんどん自分で進めていく力が彼の武器だと思います。もちろん、これから何度も壁にぶつかることはあると思いますが、その壁を乗り越えながら進んでくれることを期待します。

池田： プログラミングは、「これが使えるようになったら便利かな」と思って、パソコンをいろいろ触って覚えました。また、数学の研究に必要な情報は、ネットで見たり本で調べたりしています。この先ずっと同じ知識のまま生きていくのではなく他の人と違うことを学び、新しい知識を身につけたいという気持ちが強いです。

宇都： 今、本校としても主体的な姿勢を大切にしています。10年以上前の浜松学芸高校は、効率を重視して詰め込み型の授業をするようなこともありましたが、今は方針を変えています。生徒には主体的に勉強してもらって、私たちはそれをアドバイスするのが基本的なスタンスです。だから彼のような活動をする生徒を見ているとワクワクします。

宇都： 科学情報コースでも数学を重視していきます。特進コースの場合は大学受験が一番の目標になるので、問題を解答する力を養うことを優先しますが、科学情報コースでは基礎的な数学を中心に行って、「面白さ」や「楽しさ」を感じてほしいと思っています。そして、生徒たちの「数学的思考力」を鍛えたいですね。

宇都： 現実の社会に役立つような思考力を、数学を通して磨くイメージです。一つ例を出すと、「消去法」というのは数学的な思考の一種と言っていいと思います。目の前にＡとＢという選択肢があったとして、一か八かでどちらかを選ぶのではなく、「Ａを選んだ場合はこうなって、Ｂを選んだ場合はこうなる」と仮説を立て、メリットとデメリットを比べて判断する。そういう考え方を知っていくことが、数学を学ぶ意義の一つだと思います。